格子定数の精密化の方法

面間距離dには単位格子の大きさを決めるすべての情報が含まれている。dと指数(hkl)との間には次の関係がある。

これを変形して、

さらに、

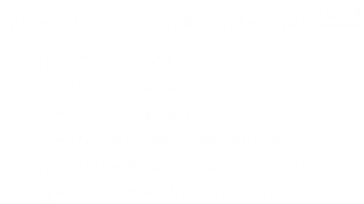
　従って、d値は6個のパラメータの関数になっている。

(hkl)の指数をもつ反射のd_hkl値（θの関数になっている）がn個観測されたとすると、9個のパラメータ（この場合は格子定数が未知、hklが既知）をもつn個の観測方程式が得られる。従って、6個以上（三斜晶系の場合）のd値の観測データがあれば格子定数は精密化できることになるが、実際には変数の10倍程度の観測データが必要である。n個の観測方程式を書くと、

ただし、

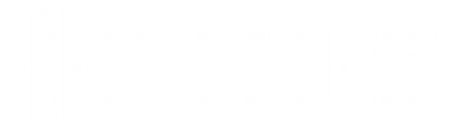
　ここで、d値の測定誤差については、

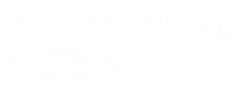
の関係があるので、高い精度の格子定数を求めるためには、高角の2θ_hklを用いることが必要である。現実的には全ての2θ_hklを用いて最小二乗法により格子定数を精密化している。一般に2θ_hklの測定値にはゼロシフトと試料変位による誤差も含まれているので、これを考慮すると

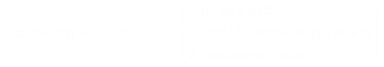
となり、従ってdhklは、

の11個の変数（未知のパラメータは格子定数とゼロシフトおよび試料変位の8個）によって表される。

　線形の最小二乗法の一般論より、

ここで、xは精密化したい変数行列、yは測定データの行列、Aは正規行列、Wは重み行列である。この関係を格子定数の場合に当てはめると、

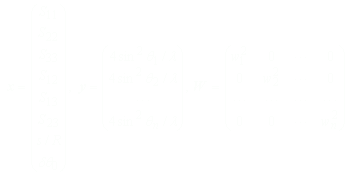
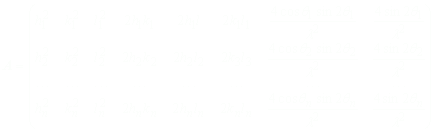
　精密化された変数（格子定数）の標準偏差は

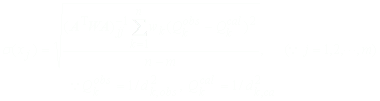
で与えられる。

　格子定数を精密化する場合に注意しなければならないことは、実測値と計算値との誤差が系統的に変化している場合には明らかにゼロ点シフトあるいは試料変位を精密化する必要があることを示している。ただし、試料変位とゼロシフトは互いに相関性が強いので、これらを同時に精密化する場合には注意が必要である。通常は同時に精密化しない。